Number system

Number System:

साधारणतः हम जिस number system का प्रयोग करते हैं, उसे Decimal number सिस्टम(दशमलव संख्या प्रद्धति ) कहते हैं। Decimal number system में 0 से 9 तक के अंक होते हैं। यह number system पूरे विश्व में प्रचलित है। परंतु computers और अन्य electronic मशीनों में decimal number system का इस्तेमाल नहीं किया जाता है। Computer के क्षेत्र में अन्य number system चलते हैं, जो कि निम्न हैं।

1. Binary number system
2. Octal
3. Hexadecimal

इन नंबर सिस्टम को समझने से पहले हम साधारण decimal system को समझेंगे क्योंकि सभी number systems की कार्यप्रणाली एक जैसे है।

Decimal Number System:

इस नंबर सिस्टम में 0 से लेकर 9 तक कुल दस चिन्ह हैं। (0,1,2,3,4,5,6,7,8,9)। माना कि हम काँच की गोलियों के एक ढेर की गिनती करना चाहते हैं। हम 1 से सुरू करते हैं और 9 पर रुकते हैं। अब सारे चिन्ह खत्म हो गए हैं। अतः 9 से आगे गिनने के लिए हम पहली वाली संख्या को बायीं(left) ओर खिसका देते हैं और दायीं और फिर से 0 से 9 तक गिनते हैं।(10, 11, 12,...................19)। अब दोबारा से दायीं तरफ की संख्या 9 पर खतम हो गए हैं। अब हम दोबारा बायीं ओर की संख्या में 1 जोड़ देते हैं और दायीं तरफ फिर से 0 से 9 तक गिनती सुरू करते हैं। (20, 21, 22, 23, 24,.............29)।

इस उदाहरण से पता चलता है की जब हमारे decimal number system के अक्षर खत्म हो जाते हैं, तब हम बायीं तरफ एक संख्या बढ़ा देते हैं, और दायीं तरफ की गिनती फिर 0 से सुरू कर देते हैं। यही नियम सभी नंबर सिस्टम पर लगता है।

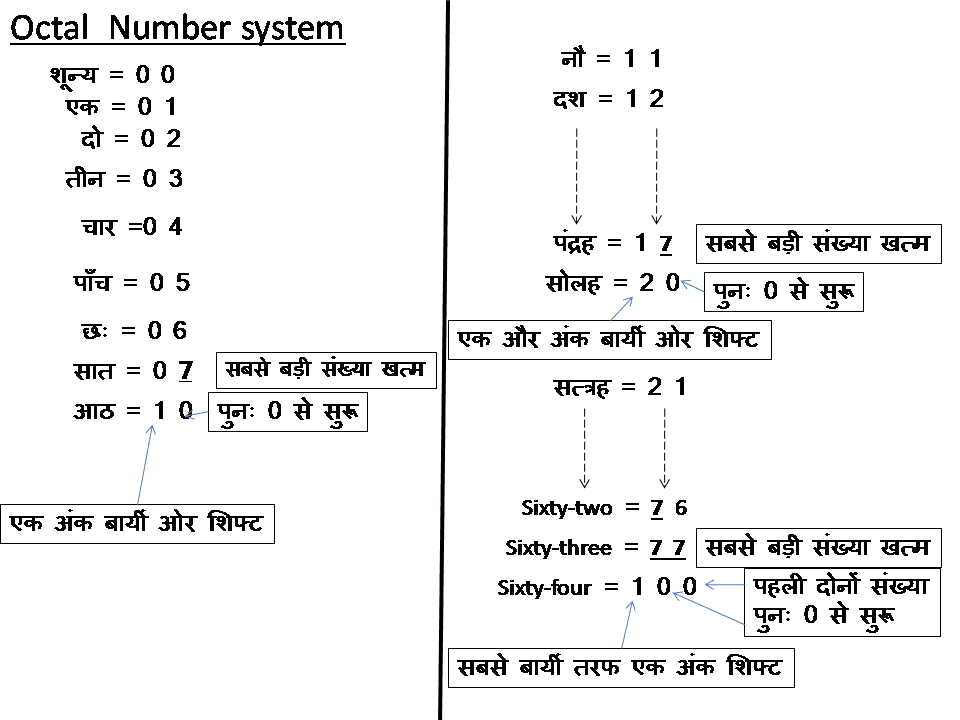
Octal Number System:

इस नंबर सिस्टम में शून्य(0) को मिलाकर केवल आठ अक्षर होते हैं। (0, 1, 2, 3, 4, 5, 6, 7)। जैसे Decimal सिस्टम में 9 के बाद कोई चिन्ह नहीं है, ठीक उसी प्रकार मान लीजिये की 7 के बाद कोई अक्षर है ही नहीं। आप 8 और 9 को पूरी तरह भूल जाइये। अब अगर आपको सात(7) के बाद आठ लिखना है तो वही प्रक्रिया यहाँ पर अपनाई जाएगी। आठ के लिए पुनः पहला अंक बायीं ओर खिसकेगा और दायीं ओर 0 से सुरू होगा। अतः यहाँ आठ को 10 और नो को 11 लिखेंगे। इसी प्रकार दस=12, ग्यारह=13, बारह=14, तेरह=15,चोदह=16, पंद्रह=17 है। यहाँ पर पंद्रह पर फिर से सबसे बड़ी संख्या खत्म हो गयी है, अतः सोलह के लिए फिर से एक संख्या बायीं ओर बढ़ेगी और दायीं ओर फिर से 0 से सुरू होगा। अतः सोलह=20 और सत्रह=21, आदि।

Hexa-Decimal Number System:

इस नंबर सिस्टम में कुल पंद्रह चिन्ह(symbol) हैं। (0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F)। यह system भी पूरी तरह decimal system की तरह कार्य करता है। 

Binary Number System:

Binary नंबर सिस्टम में केवल दो चिन्ह होते हैं, (1 और 0)। '0' का मतलब 'OFF' और '1' का मतलब 'ON' है। बाइनरि नंबर सिस्टम को मशीनी भाषा भी कहते हैं। क्योंकि किसी भी मशीन के साथ दो ही कम किए जा सकते हैं। या तो ON करो या OFF करो। Electric machine सिर्फ वोल्टेज और करेंट से चलती हैं। जब हम किसी computer को कोई काम करने की command देते हैं, तब कम्प्युटर अपने सेकड़ों पुर्जों को 0 और 1 की भाषा में on और off करके सही output देता है। यह नंबर सिस्टम भी Decimal नंबर सिस्टम की तरह कार्य करता है। Binary सिस्टम में सबसे छोटी संख्या 0 है और सबसे बड़ी 1 है।

Redix या आधार या Base

अभी तक हमने ऊपर के अध्याय में चार नंबर सिस्टम पढे हैं। प्रत्येक सिस्टम में इस्तेमाल होने वाले कुल चिन्ह, उस नंबर सिस्टम का आधार होता है।

1. Decimal नंबर सिस्टम में 0 से 9 तक कुल दस चिन्ह होते हैं। अतः इस सिस्टम का आधार या Redix '10' है। माना की कोई संख्या 2879 है। अतः redix के साथ इस संख्या को इस तरह लिखेंगे (2879)₁₀
2.  Octal नंबर सिस्टम में 0 से 7 तक कुल आठ चिन्ह होते हैं। अतः इस सिस्टम का आधार '8' है। Example: (2357)₈
3.  Hexadecimal नंबर सिस्टम में 0 से F तक कुल सोलह चिन्ह होते हैं। अतः इसका redix '16' है। Example: (369AD)₁₆
4. Binary नंबर सिस्टम में 0 और 1 को मिला कर कुल दो चिन्ह हैं। अतः बाइनरि का redix '2' है। Example: (1011)₂

Conversion of one Number System Into Another

एक नंबर सिस्टम का दूसरे नंबर सिस्टेम में रूपान्तरण।

1. Octal to Decimal
2. Hexadecimal to Decimal
3. Binary to Decimal

सबसे पहले हम डेसिमल नंबर को लिखने के तरीके पर ध्यान देंगे। माना कि  (3568.354)₁₀ कोई डेसिमल संख्या है, जिसका आधार(Redix) 10 होता है। इसमे सबसे बायीं तरफ  '3' सबसे बड़े स्थान की संख्या है अतः '3' को Most Significant Digit (MSD) कहेंगे, जबकि सबसे दायीं तरफ '4' सबसे छोटे स्थान पर है, अतः '4' को Least Significant Digit(LSD) कहेंगे। इस संख्या में कुल सात अंक हैं।

• अब हम इस संख्या के सभी अंकों की numbering करेंगे। Point से बायीं ओर MSD की तरफ बढ़ते हुए पहली संख्या '8' को 0 स्थान देते हैं। इसी तरह '6' को 1st, '5'को 2nd और '3' को 3rd स्थान देते हैं। यदि point से पहले और अधिक संख्या होती तो भी numbering इसी तरह और आगे बढ़ती। Point के बाद की संख्याओं की numbering '-'(ऋण) से सुरू की जाती है। अतः '3' को -1, '5' को -2 और '4' को -3 स्थान प्राप्त होता है।
• अब प्रत्येक संख्या के लिए दिये गए स्थान(numbering) को Redix (आधार) की power लगाकर उसी संख्या से गुणा कर देना है। (3×10³), (5×10²), (6×10¹), (8×10⁰), (3×10^-1), (5×10^-2), (4×10^-3)
• अब हम सभी सभी संख्याओं को हल करके एक साथ जोड़ देंगे। (3000)+(500)+(60)+(8)+(0.3)+(0.05)+(0.004)
• अब हमे जोड़ के बाद जो संख्या प्राप्त होगी वह एक डेसिमल संख्या है। = 3568.354

यदि हम उपरोक्त उदाहरण की तरह दूसरे नंबर सिस्टम को solve करें तो अंत में सबका result(उत्तर) डेसिमल नंबर सिस्टम में प्राप्त होगा।

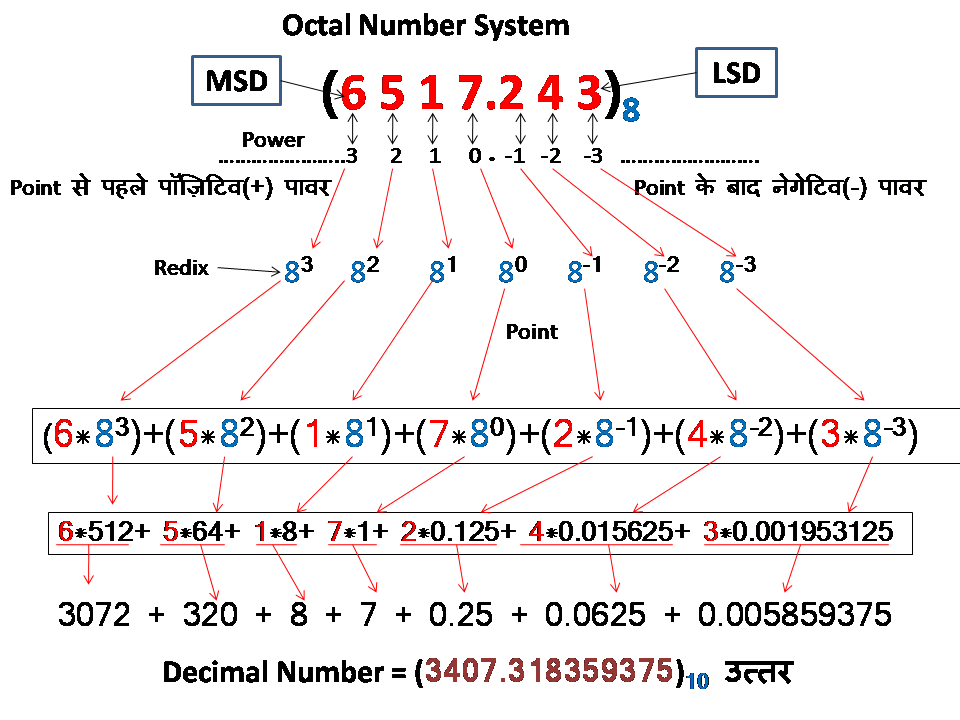
Octal नंबर सिस्टम to Decimal नंबर सिस्टम:

(6517.243)₈ को डेसिमल में convert करना:

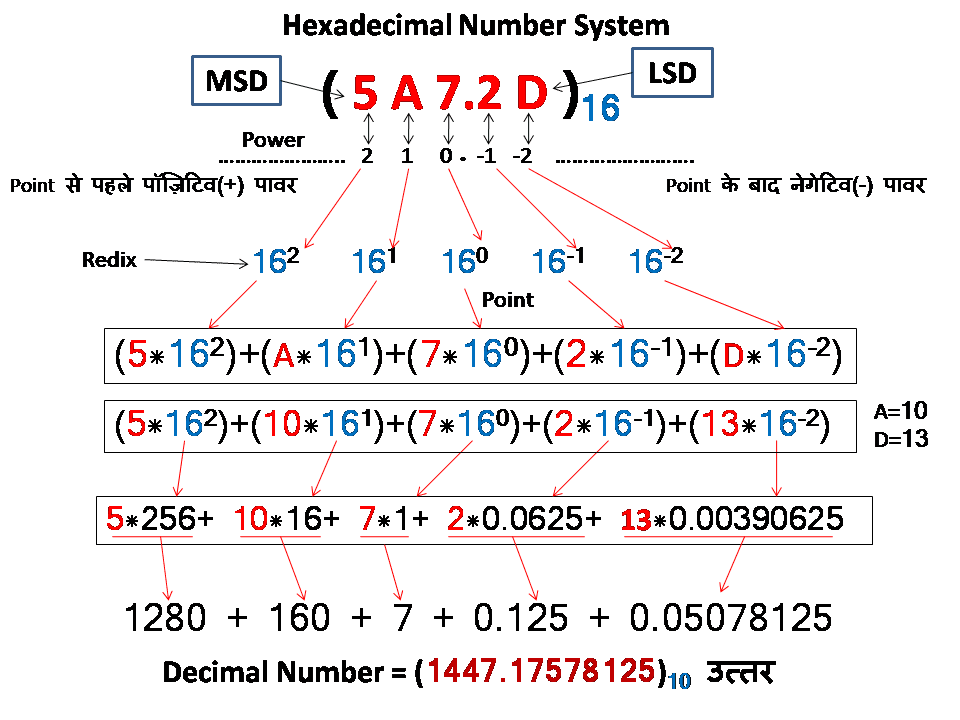
Hexadecimal to Decimal: नंबर सिस्टम:

:

Binary to Decimal नंबर सिस्टम:

Conversion of Decimal number into other number system:

1. Decimal into Octal
2. Decimal into Hexadecimal
3. Decimal into Binary

1)- Decimal into Octal number system: Example:- (3407.318)₁₀ = (?)₈

Decimal नंबर सिस्टम को Octal सिस्टम में convert करने के लिए, point से पहले वाली संख्या को और point के बाद वाली संख्या को अलग-अलग तरीके से convert किया जाता है। Point से पहली वाली संख्या को, जिस नंबर सिस्टम में convert करना है, उस नंबर सिस्टम के Redix (यहाँ Octal system के Redix(8)) से, Quotient(Q) के अंत में शून्य आने तक भाग(Divide) करते हैं। प्रत्येक बार भाग देने पर जो भी शेष(reminder) बचता है(चाहे वह शून्य ही क्यों न हो), उसे एक तरफ लिखते जाते हैं। आखिरी में जब divide करने के लिए कुछ भी नहीं बचता है, तब सभी शेषफल को उल्टी तरफ से उत्तर में लिखते हैं।

Point से बाद की संख्या को जिस नंबर सिस्टम में convert करना हो, उसी नंबर सिस्टम के redix से multiply करते हैं। (यहाँ octal में कन्वर्ट करने के लिए '8' से multiply करेंगे)। हर बार multiply करने पर जो भी carry पॉइंट के बायीं ओर shift होता है, उसे अलग लिख लेते हैं। अन्त में उत्तर को पहले carry से last carry की ओर लिखते हैं।

Decimal system को अन्य सभी सिस्टम में convert करने के लिए same process है।

2)- Decimal to Hexadecimal:   (1447.17578)₁₀ = ( ? )₁₆

_{3)- Decimal System to Binary system:} (11.375)₁₀ = ( ? )₂

सभी नंबर सिस्टम का अध्यन करने के बाद हमे पता चलता है, कि computers में octal(0to7), hexadecimal(0toF) और binary सिस्टम का स्तेमाल किया जाता है, जबकि डेसिमल सिस्टम का प्रयोग सिर्फ output display करने के लिए किया जाता है। इसके कारण निम्न हैं।

Output डिस्प्ले)- साधारणतः हम लोगों को 0 से 9 तक के combination से बने decimal नंबर  कि गिनती ही समझ मे आती है, क्योंकि ये अन्य नंबर सिस्टम से ज्यदा आसान है, अतः computers की output को दर्शाने के लिए decimal number system का use किया जाता है।
Binary system)- Computer के सभी function, voltage और current से चलते हैं। अतः computer के circuit, 0 या 1 (on या off) की भाषा समझते हैं। इसलिए कम्प्युटर में बाइनरि का use किया जाता है।
Octal system)- Octal में 0 से 7 तक कुल आठ नंबर होते हैं। कम्प्युटर में इनका उपयोग भी binary के रूप में किया जाता है। उदाहरण के लिए माना कि circuit में केवल 3 wire हैं। प्रत्येक wire में दो ही स्थिति हो सकती हैं। या तो wire में voltage होगी, या नहीं होगी। यदि voltage होगी, तो उसे binary का 1 माना जायेगा और यदि नहीं होगी तो उसे binary का 0 माना जायेगा। इस तरह केवल दो स्थिति के साथ 3 wires में कुल 2³=8  (आठ) conditions हो सकती हैं। इसलिए तीन तारों(wires) के circuit से, Octal number system का पूरा उपयोग किया जा सकता है।

7 से अधिक बड़ा नंबर(8 और 9) display करने के लिए circuit में wire की संख्या और बढ़ानी पड़ेंगे। 

Hexadecimal system)- Octal की ही तरह hexadecimal को भी binary के द्वारा प्रदर्शित किया जाता है। परंतु इसमे 0 से F तक कुल सोलह चिन्ह होते हैं। इसलिए इसे binary में represent करने के लिए चार wires की जरूरत पड़ती है। 

Binary     Hexadecimal

0000               0

0001               1

0010               2

0011               3

0100               4

0101               5

0110               6

0111               7

1000               8

1001               9

1010              A

1011              B

1100              C

1101              D

1110              E

1111              F

ऊपर के example से हमने देखा की octal के लिए circuit में केवल 3 wire चाहिए। जबकि इससे अधिक यानि decimal और hexadecimal के लिए 4 wire की जरूरत है। यदि 4 wire में decimal का उपयोग करते हैं, तब 4 wire में 6 combination फालतू (useless) बच जाते हैं (1010 से 1111 तक)। अतः परिपथ(circuit) का भरपूर उपयोग करने के लिए decimal system की जगह hexadecimal system का उपयोग करना ज्यादा फायदेमंद रहता है।

Note:- octal, decimal या hexadecimal में होने वाली संख्या या चिन्ह को 'digit' कहते हैं अर्थात 0,1,2,3,4,5........9,A,B,C,D,E,F सभी digits हैं जबकि binary में सिर्फ दो संख्या या चिन्ह 0 और 1 होते हैं, इन्हे 'bit' कहते हैं। अतः binary में केवल दो प्रकार की bit होती हैं।

Binary में आठ bit का एक 'Byte' होता है। अर्थात 0101 या 1111 या 1010 सभी एक Byte की संख्या हैं।

इसी प्रकार

1024 byte = 1 Kb या 1 killo byte

1024 Kb = 1Mb या 1 mega byte

1024 Mb = 1Gb या 1 Gega byte

1024 Gb = 1Tb  या 1 Terabyte

Type of Binary Codes: Binary codes निम्न प्रकार के होते हैं।

1:- Binary code:- साधारण binary codes को 0 और 1 के combination से लिखा जाता है। संख्या जितनी बड़ी होती जाती है, 0 और 1 की serise उतनी ही बड़ी होती जाती है। उदाहरण के लिए single 0 या 1 के लिए केवल 1 bit चाहिये, पर 2 के लिए बाइनरि में 10 यानि दो bit चाहिये। इसी प्रकार 8 को लिखने के लिए 1000 यानि चार bit चाहिये। अतः जितनी बड़ी संख्या होगी, उसकी bits को  transmit करने के लिए उतना ही बड़ा circuit(उतनी ही ज्यदा wire) चाहिये। अतः साधारण binary code का उसे नहीं किया जाता है।

2:- BCD या 8421 codes:- BCD का मतलब Binary coded decimal है। ऊपर हमने पढ़ा कि octal हो या decimal या फिर hexadecimal, सभी की प्रत्येक डिजिट को बाइनरि में लिखने के लिए केवल चार bits की जरूरत पड़ती है। सबसे छोटी digit 0 को बाइनरि की चार bits में 0000 लिखते हैं और सबसे बड़ी hexadecimal की सबसे बड़ी digit F(पंद्रह) को binary bits के रूप में 1111 लिखते हैं। अतः यहाँ प्रत्येक डिजिट को चार-चार bits के समूह में अलग-अलग लिखा जाता है।

example:- 237 को BCD में लिखने के लिए 2=0010, 3=0011, 7=0111

                 237= (0010 0011 0111)BCD है।

BCD या 8421 code एक weighted code है। (क्योंकि यहाँ, once, tense, hundred और thousand के रूप में सभी digits का निश्चित मान है। 237 में 7, once के स्थान पर है जबकि 3, tense के और 2, hundred के स्थान पर है।)

BCD codes को साधारणतः digital codes को decimal रूप में(0 से 9 तक) output या input लेने के लिए स्तेमाल किया जाता है। कैल्कुलेटर व अन्य डिजिटल meter में इनका प्रयोग encoder और decoder में होता है।

8421:- किसी भी चार bit की बाइनरि संख्या को 8421 की मदद से डेसिमल में आसानी से बदला जा सकता है। example:- (1001)₂ को अगर 8421 के साथ मिला कर देखें तो 8 की जगह पर 1 है और 1 की जगह पर भी 1 है, अतः (1001)₂ = 8+1=(9)₁₀  है। इसी प्रकार (1100)₂ में 8 की जगह पर 1 है और 4 की जगह पर भी 1 है, अतः (1100)₂=8+4=decimal रूप में(12)₁₀ या hexadecimal रूप में (C)₁₆ है।

3:-Excess-3 code(XS-3):- BCD code की प्रत्येक डिजिट में 3 add करके XS-3 कोड़े प्रपट किया जाता है।

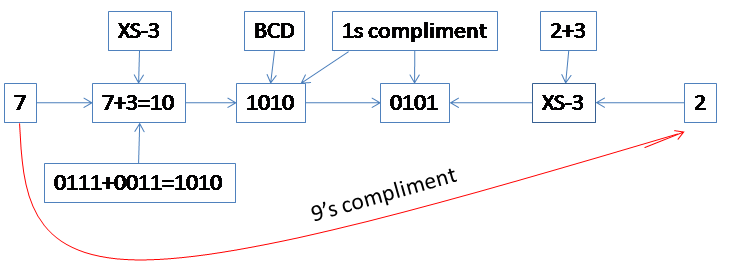
Example:- 7 का XS-3 code 7+3=10 है। BCD में 0111 का XS-3 code 0111+0011=1010 है। 

Example:- 35 का XS-3 code 3+3 और 5+3 = 68 है। BCD में 0011+0011 और 0101+0011 =0110 1000 है।

(binary में 1+1=10 जहां 1=carry और 0=sum है और 1+0=1 होता है।)

Application:- किसी भी डेसिमल संख्या के XS-3 code का 1s compliment, उस decimal संख्या के 9s कॉम्प्लिमेंट के XS-3 code के बराबर होता है।

XS-3 code, un-weighted code है क्योंकि XS3 में लिखा गया code की सही value code से अलग होती है।

XS-3 में संख्या के असली मान को को 3 बढ़ा कर लिखा जाता है।

4:- ASKII Codes:- पहले समय में जब computer का आविष्कार हुआ था, तब सभी computer निर्माता अपने computers में अपने-अपने कोड उसे करते थे। यदि किसी customer का computer खराब हो जाए तो customer को उसी computer निर्माता से ठीक करवाना पड़ता था। एक कम्प्युटर का data दूसरे computer निर्माता के computer से match नहीं होता था। इन सभी समस्याओं को दूर करने के लिए सबने मिलकर एक नया code तैयार किया जो की सूचना के आदान-प्रदान के लिए अमेरिका द्वारा प्रमाणित किया गया। इसी code को America Standard Code for Information Interchange (ASKII) कहा गया। ASKII codes के अंतर्गत अक्षरों, संख्याओं, और कुछ विशेष चिन्हों को binary के code दिये गये।

5:- Gray Code:- यह एक कम स्तेमाल होना वाला un-weighted code है। साधारणतः अन्य बाइनरि codes में एक number से बगल के दूसरे नंबर पर जाने में एक से अधिक bit बादल जाती हैं, परन्तु ग्रे code में केवल एक bit बदली होती है।

example:-बाइनरि में 7 से 8 मे जाने के लिए 0111 से 1000 में पहली bit 0 से 1 और बाकी तीन bits 1 से 0 में बादल गयी परन्तु ग्रे कोड में 7 को 0100 और 8 को 1100 लिखते हैं अतः 0100 से 1100 में जाने पर केवल पहली bit 0 से 1 में बदली हुई है और बाकी सभी bits same हैं।

BCD to Gray conversion:

Gray to BCD conversion:

_{Next chapter: Addition and subtraction of Number systems.}